Die Bestimmung der Sonnenscheindauer anhand des Schattenwurfs

Seit 1989 ist die Sonnenscheindauer von der WMO definiert als die Länge derjenigen Zeit, während der die direkte Sonnenstrahlung mehr als 120 W/m² beträgt. Um dies zu messen, muss folglich die indirekte Strahlung ausgeblendet werden. Ein geeignetes Messinstrument besteht also aus einem Rohr, das auf die Sonne hin ausgerichtet ist, an dessen Ende eine Sonnenzelle die einfallende Strahlungsenergie misst. Da die ständige Ausrichtung in Richtung Sonne sehr aufwendig ist, sind solche Messgeräte (Pyrheliometer) selten.

Messtechnisch einfach zu erfassen ist die gesamte (direkte und indirekte) Strahlungsenergie, die auf eine horizontale Fläche fällt (Pyranometer). Von Metereologen des Königlich Niederländischen Dienstes wurden Algorithmen entwickelt, die aus diesen Messdaten einen Näherungswert für die Sonnenscheindauer nach der WMO-Definition berechnen (s. Slob & Monna 1991, Hinssen & Knap 2007). Beide Näherungsalgorithmen werden mit den Daten der LOG-Wetterstation durchgeführt.

Eine andere Herangehensweise wäre folgende: Es wird definiert: zu einem Zeitpunkt herrscht Sonnenschein, wenn Objekte einen Schatten werfen. Um auf diese Weise die Sonnenscheindauer zu bestimmen, habe ich ein Umbraskop konstruiert (die Bezeichnung Umbraskop wurde schon einmal verwendet für eine Vorrichtung, die es gestatten sollte, zu messen, wie verräuchert die Luft ist, vgl. hier. Da sich dieses Gerät nicht durchgesetzt hat, wird die Bezeichnung hier neu bestimmt.)

Das Umbraskop besteht aus einer vertikalen Stange, die ihren Schatten auf eine horizontale Fläche wirft. Über der Stange hängt eine Webcam. Einmal pro Minute nimmt die Webcam ein Bild auf, vgl. die Abbildung 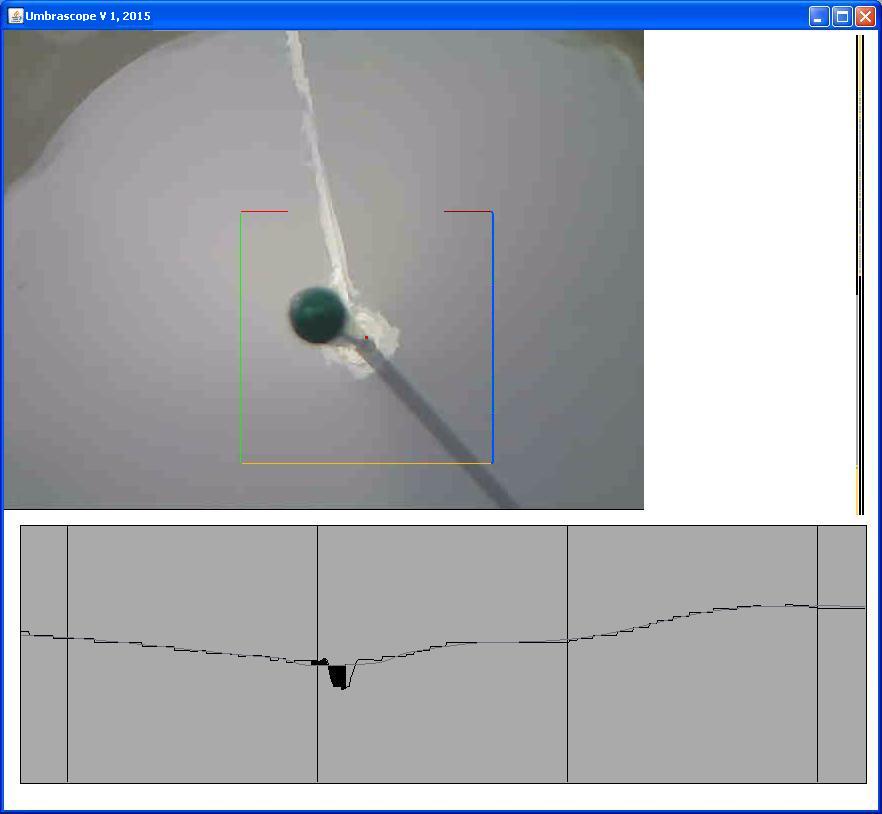. Eine Software bestimmt die Helligkeit der Pixel des Bildes auf einer Linie, die um den Fußpunkt der Stange herumführt. Dort, wo der Schatten hinfällt, ist der Helligkeitswert der betreffenden Pixel geringer, was durch einen Vergleich mit einem gleitenden Mittelwert über die auf der Messlinie benachbarten Pixel festgestellt wird (vgl. die Graphik auf der Abbildung unten).

Problematisch ist, dass ein Schwellenwert festgelegt werden muss, ab dem ein Helligkeitsunterschied zwischen beleuchteter und verschatteter Fläche als signifikant zu betrachten ist. Die Software erlaubt es, diesen Schwellenwert zu kalibrieren.

Die statistische Auswertung der bislang gesammelten Bruchköbler Daten (Stand: 22.2.2016; 195 Datenpunkte Umbraskop, 583 Datenpunkte Slob & Monna, 663 Datenpunkte Hinssen & Knap) ergibt folgende Korrelationskoeffizienten:

Slob & Monna vs. Hinssen & Knap:	0,8978
Slob & Monna vs. Umbraskop:	0,9255
Hinssen & Knap vs. Umbraskop:	0,9573