Ebenengleichung (Parameterform)

Himmelheber, 21.11.9, erstellt mit GeoGebra

Ganz ähnlich wie bei der Geradengleichung gibt es auch zur Darstellung von Ebenen mit Hilfe der Vektorrechnung eine Parametergleichung. Betrachten wir folgendes Beispiel:

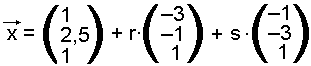
Formel

Wie bei der Geradengleichung gibt es einen Stützvektor und 2 weitere Vektoren, die dem Richtungsvektor bei der Geradengleichung entsprechen. Ferner gibt es 2 Parameter, r und s. Indem diese Parameter von minus unendlich bis plus unendlich variieren, erreicht der Vektor x jeden Punkt der dargestellten Ebene.

In der Darstellung hier erkennen Sie den Stützvektor a (alle Vektoren sind hier ohne Pfeil drüber wiedergegeben) und die „Richtungsvektoren“ m und n, die die Ebene aufspannen. Dann gibt es rechts noch zwei Schieberegler, mit denen die Parameter r und s eingestellt werden können (allerdings nur im Bereich von –1 bis 2). Je nach Reglerstellung ergibt sich also ein anderer Wert des Parameters, mit welchem der jeweilige Richtungsvektor gestaucht oder gestreckt wird.

Aus der Summe der drei (ggf. mit dem jeweiligen Parameter mutliplizierten) Vektoren ergibt sich der rote Vektor x, der als Ortsvektor zum Ebenenpunkt E zeigt.

Spielen Sie ein wenig mit den Schiebereglern und beobachten Sie den Ortsvektor des Punktes E. Versuchen Sie, das ganze räumlich zu sehen.

Ebenso, wie es bei der Geradengleichung möglich war, zu zwei gegebenen Punkten die Geradengleichung aufzustellen, kann man auch hier, wenn 3 Punkte gegeben sind, die Ebenengleichung (in der Parameterform) aufstellen.

Aufgabe: Wie bekommt man die Richtungsvektoren? Gibt es mehrere Möglichkeiten?

Es seien die drei Ortsvektoren zu den drei Punkten a, b, c. Stellen Sie in den Kästchen 2 mögliche Richtungsvektoren dar.